フロンティアバイオサイエンス学科
 西郷 甲矢人(さいごう・はやと)
西郷 甲矢人(さいごう・はやと)
Hayato Saigo
専門分野/数理物理(代数的確率論)研究キーワード/代数的確率論、量子古典対応、圏論
職位:教授
学位:博士(理学)(京都大学)
- 京都大学理学研究科(数学・数理解析専攻)博士課程修了
- プリンストン高等研究所(Interdisciplinary Studies, 2010-2011期)滞在後本学へ
研究テーマ
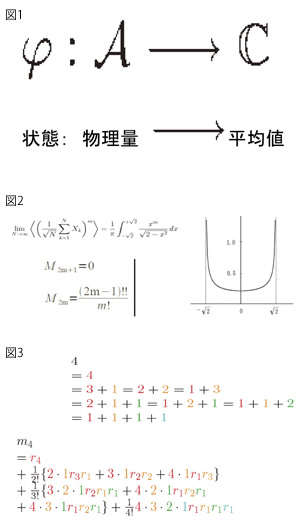
自然界には、偶然的に「ゆらぐ」量が満ち溢れています。偶然的というのも、「本当は必然的だが我々が無知」という場合ばかりではありません。たとえば、電子の位置や運動量といった物理量のゆらぎの偶然性は、無知のせいにはできないことが知られています。それでも、「一定の状態のもとでは」ゆらぎの傾向に法則が現れます。値は確定しなくても平均値なら決まる、というように。この場合、ゆらぎ方の傾向を定める「状態」は、物理量に対して平均値を対応させる関数としてとらえられます。(図1)
電子のゆらぎなどにおける偶然性を「無知のせいにできない」という事実は、物理量の積について「AB=BA とは限らない」という「代数的」な構造に根ざしていることが知られています。私は、自然の根底に流れるこのような数理を探るために、代数的な観点からゆらぎを研究する理論=「代数的確率論」を研究しています。
(1)量子古典対応の数理
代数的確率論を背景に、ボルンの確率規則、相補性、光子の局在化などに関する数理的研究を進めている(小嶋泉氏、岡村和弥氏らと共同)。さらに私は、「量子古典対応」(ミクロの法則とマクロの法則のつながり)の数理において「逆正弦法則」という分布(図2)が果たす重要な役割を代数的確率論によって研究している。
(2)新しい「独立性」概念
代数的確率論では、「独立性」の概念が多様化する。中でも「単調独立性」に関しては、通常の独立性において「正規分布」が果たす役割を、「逆正弦法則」が担う。単調独立性は、XがYに対して独立であるからといって、YがXに対して独立とは限らない、という特性を持つ。私はこれに起因する組合せ論的構造(図3)を発見し、長谷部高広氏と共に「一般化キュムラント」の概念を得た。
(3)圏論による組織化
独立性の概念を始め、代数的確率論では、これまでの「ゆらぎの解析」で育まれた概念の「自然な一般化」を考える必要が生ずる。この「自然な一般化」の意味を明確にするのが、「圏論」という数学の一分野である。私は、ゆらぎの解析を組織化する(そして異分野とのつながりを発見する)ための圏論的な方法についても研究している。
| 研究の応用領域 | 産官学連携で求めるパートナー |
|---|---|
| 代数学・組み合わせ論・確率論から自然科学における数理モデルの研究まで多岐にわたる。 | 自然に満ち溢れるゆらぎを無理矢理に押さえ込もうとするのではなく、ゆらぎと巧みに付き合い、むしろそれを活かしていくような文化・技術を志向する方々。 |
Topics of research
Algebraic probability is such an algebraic framework extending probabilistic notions that its scope is to cover various areas of mathematics and sciences related to quantum theory.
While usual probability theory mainly treats random variables commuting with each other, in quantum theory it is essential to deal with noncommutative random variables which we call observables. Then states are nothing but the expectation functionals for noncommutative random variables.
Conceptually, an algebra of observables describes the system to be observed and a state an interface between observed and observing sides (a view point due to I. Ojima). By taking this point of view, we can obtain a deeper understanding of the fundamental problems in Physics. For instance, we have discovered the crucial role of the "Arcsine Law'', a famous probability law, in "Quantum-Classical Correspondence".
One of the central issues of interest in algebraic probability as a mathematical theory is the extension of the notion of "independence".
Among many kinds of generalizations "monotone independence" (Muraki) is a unique one as an "asymmetric" kind characterized by certain naturality conditions, in the sense that monotone independence of "X from Y" does not imply that of "Y from X". The monotone version of Central Limit Theorem (CLT) is first obtained by Muraki, with its "limit distribution" not being the Gaussian but the Arcsine law.
We have succeeded in clarifying the intrinsic combinatorial structure of monotone limit theorems for the first time.
What is the most relevant to the unification of such types of the limit theorems is the notion of "cumulants", which is, however, incompatible with the above sort of asymmetry inherent in the monotone independence. This was the most essential obstruction which prevented the transparent explanation for the logical relation between monotone CLT and the definition of monotone independence. In collaboration with T. Hasebe, we have overcome this difficulty by our discovery of "generalized cumulants" By the use of this, we have obtained quite simple proofs for the limit theorems in the monotone case.
Moreover, the combinatorial representation of the relation between moments and generalized cumulants are obtained by developing the arguments before due to myself. Now we are investigating the category-theoretic meaning of generalized cumulants.
主な業績論文等
- I. Ojima, K. Okamura and H. Saigo, Derivation of Born Rule from Algebraic and Statistical Axioms, Open Systems and Information Dynamics, 21, 1450005 (2014).
- T. Hasebe and H. Saigo, On operator-valued monotone independence, Nagoya Mathematical Journal, 215, 151-167 (2014).
- H. Saigo, A new look at the Arcsine law and “Quantum-Classical Correspondence”, Inf inite Dimensional Analysis, Quantum Probability and Related Topics, 13,1250021 (2012).
- I. Ojima and H. Saigo, Who has seen a free photon?, Open Systems and Information Dynamics 19, 1250008 (2012).
- T. Hasebe and H. Saigo, The monotone cumulants, Annales de l’Institut Henri Poincaré;(B) Probabilités et Statistiques 47, No. 4, 1160-1170 (2011).






